算法上机复习
本文最后更新于:3 年前
最近算法实验要上机考试,所以还是准备一下吧(还不是因为自己太菜了)
16级题目
问题 A: 星空梦想——鲁班
题目描述
鲁班七号是王者峡谷里的射手,站撸英雄。战场上的鲁班七号,机制强大的鲨嘴炮,立刻将挡在前路的任何物体轰飞。正如他所说的,“借你们的肉体试验下新发明的威力”。是的,这就是鲁班大师和他的天才机关造物鲁班七号。然而,鲁班最为致命的缺点是腿短,跑得慢,一个稍不留神,便会被刺客所击杀。
既然腿短,那么就来多多运动吧,跳跳台阶可还行?假设鲁班七号一次可以跳上1级台阶,但极限一次只能跳上2级台阶(腿短没办法,嘤嘤嘤)。鲁班七号现在从0级阶梯开始,最终跳上第n级的台阶,求总共有多少种跳法?
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=50),代表测试用例个数。
接下来T行,每行输入包含一个整数n(1<=n<=50),代表鲁班最终跳上了第n级台阶。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表鲁班最终跳上第n级台阶的跳法种数。
样例输入
3
3
4
50样例输出
3
5
20365011074提示
注意结果超过int范围,请用long long类型存储ans
#include<bits/stdc++.h>
using namespace std;
const int N=50;
long long f[N];
int main()
{
f[0]=1,f[1]=1;
for(int i=2;i<=50;i++)
{
f[i]=f[i-1]+f[i-2];
}
int n;
cin>>n;
while(n--)
{
int m;
cin>>m;
cout<<f[m]<<endl;
}
return 0;
}
问题 B: 午夜歌剧——元歌
题目描述
元歌是王者峡谷里的刺客。何谓至高机关之美呢?唯有以至高权力的手令太古奇迹重现人世,方能称得上啊。
是的,元歌擅长操控,所做傀儡能起到以假乱真的作用,今天元歌的傀儡变成你的初中数学老师,给你出个数学题:给你一个数字x,让你求出k7、k6、k5、k4、k3、k2、k1、k0(0<=ki<=9),使得以下等式1成立,最后根据等式2求出最终ans值。
等式1:
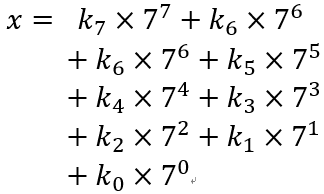
等式2:
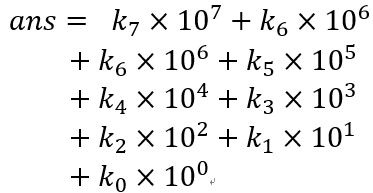
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=1000),代表测试用例个数。
接下来T行,每一行包含一个整数x(1<=x<=1500000)。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表最终运算结果。
样例输入
3
7
143
3223193224样例输出
10
151
163311433223提示
测试数据均大于等于1,不用特判0
感觉图片等式有点问题,一开始没理解什么意思,后来看了学长的提示。本质就是进制转换。
#include<bits/stdc++.h>
using namespace std;
int t,m;
void convert(int n)
{
int c,r;
r=n%7;
c=n/7;
if(c>0)
{
convert(c);
cout<<r;
}
else
cout<<n;
}
int main()
{
cin>>t;
while(t--)
{
cin>>m;
convert(m);
cout<<endl;
}
return 0;
}问题 C: 圣诞恋歌——貂蝉
题目描述
貂蝉是王者峡谷里的法师/刺客,貂蝉打法一定要注意配合技能与被动。半肉出装加上蛇皮走位,往往可以1打5,轻松拿下5杀。语花印被动描述为:技能命中会为敌人叠加花之印记,叠加满4层后印记触发被动,会给自身回复生命,同时会对周围敌人造成真实伤害并减速。
我们现在对貂蝉的技能及被动进行简化如下:每使用1次技能会攻击1次目标,每攻击3次目标,会自动额外攻击1次目标。
现在,貂蝉在游戏中使用了n次技能,请问总共会给目标带来多少次攻击。
输入
多组测试数据,第一行输入包含一个整数T,代表测试样例个数。
接下来T行,每行输入包含一个整数n(1<=n<=100),代表貂蝉使用了n次技能。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表貂蝉对目标进行了ans次攻击。
样例输入
6
1
2
3
45
81样例输出
1
2
4
57
121提示
这题就是汽水瓶的改编。。。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
while(n--)
{
int m,sum;
cin>>m;
sum=0;
while(m>3)
{
m=m-2;
sum=sum+3;
}
if(m==3)
sum+=4;
else
sum=m;
cout<<sum<<endl;
}
return 0;
}问题 D: 海之征途——孙策
题目描述
孙策是王者峡谷里的坦克/战士。大船靠岸,江郡欢呼着迎来了他们的新领袖,人称江东小霸王的年轻人。游戏中,孙策的技能长帆破浪,可以驾船冲锋,可将船撞向敌方单位或者阻挡物,并造成一定的伤害。
现在,有一群好奇的江郡小朋友想跟着孙策一起出海航行,但孙策的船承载不了所有小朋友,所以孙策决定,尽可能带更多的小朋友出海,现在请你帮孙策谋一个策略,使得更多的小朋友有机会出海航行。已知的条件是孙策船的最大载重m,以及n个小朋友的体重。
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=1000),代表测试用例个数。
每组测试用例第一行有两个整数m和n。(0<=m<=1000, 0<=n<=1000),分别代表船的载重重量和小朋友的个数,接下来一行为n个小朋友的体重。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表最多能有ans个小朋友跟着一起出海。
样例输入
2
10 4
3 5 2 4
20 9
3 5 2 4 6 1 8 5 9样例输出
3
6提示
就是简单的装在问题
#include<bits/stdc++.h>
using namespace std;
int T,m,n;
int w[1005];
int main()
{
cin>>T;
while(T--)
{
int ans=0;
cin>>m>>n;
for(int i=0;i<n;i++)
{
cin>>w[i];
}
sort(w,w+n);
for(int i=0;i<n;i++)
{
if(m>=w[i])
{
ans++;
m-=w[i];
}
else
break;
}
cout<<ans<<endl;
}
return 0;
}问题 E: 极冰防御——盾山
题目描述
盾山是王者峡谷里的辅助,一夫当关、万夫莫开,一个好的辅助往往可以给团队带来极大帮助。
盾山的游戏中的一个技能为不动如山:手握一块由石头组成的巨盾,张开巨盾砸向地面,将敌人推开,并持续一段时间。
假设盾山最多只能承受C重量的盾牌,而现在有N个小石头,每个石头i的重量为Wi,防御值为Pi。那么,呆萌的盾山想知道,他从N个小石头中挑选M个(M<=N)组成他可承受盾牌,最大的防御值是多少?
输入
多组测试用例。
第一行输入包含一个整数T(1<=T<=10),代表测试用例个数。
接下来有T组测试用例。每组测试用例第一行为盾山承受盾牌的最大重量C(C<10000)和小石头的个数N(N<1000)。接下来的N行分别为小石头的重量Wi(1<=Wi<=100)和防御值Pi(1<=Pi<=3000000)。
输出
每组测试用例对应一行输出,每行输出一个整数ans,代表可承受盾牌的最大防御值。
样例输入
1
10 5
2 6
2 3
6 5
5 4
4 6样例输出
15提示
01背包问题,不知道下面的解能不能过
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
long long ans[N];
int w[N],v[N];
int T;
int main()
{
cin>>T;
while(T--)
{
int C,N;
memset(ans,0,sizeof(ans));
cin>>C>>N;
for(int i=0;i<N;i++)
{
cin>>w[i]>>v[i];
}
for(int i=0;i<N;i++)
{
for(int j=C;j>=w[i];j--)
ans[j]=max(ans[j-1],ans[j-w[i]]+v[i]);
}
// for(int i=0;i<=C;i++)
// cout<<ans[i]<<endl;
cout<<ans[C]<<endl;
}
return 0;
}ps:以上代码没有提交测试环境,只是过了给出的测试样例。
dfs大合集
迷宫问题
题目描述
小明置身于一个迷宫,请你帮小明找出从起点到终点的最短路程。
小明只能向上下左右四个方向移动。
输入
输入包含多组测试数据。输入的第一行是一个整数T,表示有T组测试数据。
每组输入的第一行是两个整数N和M(1<=N,M<=100)。
接下来N行,每行输入M个字符,每个字符表示迷宫中的一个小方格。
字符的含义如下:
‘S’:起点
‘E’:终点
‘-’:空地,可以通过
‘#’:障碍,无法通过
输入数据保证有且仅有一个起点和终点。
输出
对于每组输入,输出从起点到终点的最短路程,如果不存在从起点到终点的路,则输出-1。
样例输入
1
5 5
s-###
-----
##---
E#---
---##样例输出
9#include<iostream>
#include<cstring>
#include<string>
#include<queue>
#include <algorithm>
using namespace std;
int de[100][100];//计步数组 记录走到这个位置所需的步数 不能走到的位置标记为-1
char map[100][100]; //用于存放迷宫地图
typedef pair<int,int> P; //坐标
int to[2][4]={1,-1,0,0,0,0,1,-1}; //在当前坐标下能走的四个方向
int sx,ex,sy,ey; //(sx,sy)为起点坐标 (ex,ey)为终点坐标
int x,y,nx,ny; //(x,y)为函数中当前位置坐标 (nx,ny)为接下来能到达的坐标
int r,l; //r为行数 l为列数
int bfs()
{
memset(de,-1,sizeof(de));
queue<P> qu;
qu.push(P(sx,sy)); //将起点坐标放入队头
de[sx][sy]=0;
while(!qu.empty())
{
P p=qu.front(); //取出队头坐标
qu.pop() ;//删除对头及走过的坐标
x=p.first,y=p.second;
if(x==ex&&y==ey) break; //到达终点 跳出循环
for(int i=0;i<4;i++)
{
nx=x+to[0][i];//开始向四个方向移动
ny=y+to[1][i];
if(nx>=0&&nx<r&&ny>=0&&ny<l&&map[nx][ny]!='#'&&de[nx][ny]==-1)
//判断是否越界 以及是否能走 排除走过的路
{
qu.push(P(nx,ny)); //将能走的坐标放入队列 之后依次删除
de[nx][ny]=de[x][y]+1; //步数加一
}
}
}
if(de[ex][ey]==-1) return -1; //终点的记步数组为-1 及不能到达终点
else return de[ex][ey];
}
int main()
{
int n,i,j;
while(cin>>n){
while(n--){
cin>>r>>l;
for(i=0;i<r;i++){
for(j=0;j<l;j++){
cin>>map[i][j];
if(map[i][j]=='S') //记录起点坐标
{
sx=i,sy=j;
}
else if(map[i][j]=='T') //记录终点坐标
{
ex=i,ey=j;
}
}
}
cout<<bfs()<<endl;
}
}
return 0;
}acwing迷宫问题
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int mp[N][N];
int dis[N][N];
typedef pair<int,int> P;
int n,m;
int to[2][4]={1,-1,0,0,0,0,1,-1};
int x,y,nx,ny;
void dfs()
{
memset(dis,-1,sizeof(dis));
queue<P> qu;
qu.push(P(0,0));
dis[0][0]=0;
while(!qu.empty())
{
P p=qu.front();
qu.pop();
x=p.first,y=p.second;
if(x==n-1&&y==m-1) break;
for(int i=0;i<4;i++)
{
nx=x+to[0][i],ny=y+to[1][i];
if(nx>=0&&nx<n&&ny>=0&&ny<m&&dis[nx][ny]==-1&&mp[nx][ny]==0)
{
qu.push(P(nx,ny));
dis[nx][ny]=dis[x][y]+1;
}
}
}
if(dis[n-1][m-1]!=-1)
cout<<dis[n-1][m-1];
return;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cin>>mp[i][j];
dfs();
return 0;
}n皇后问题
#include<bits/stdc++.h>
using namespace std;
int n,ans=0;
const int N=20;
char m[N][N];
bool col[N],dg[N],udg[N];
void dfs(int u)
{
if(u==n)
{
// for(int i=0;i<n;i++)
// cout<<m[i]<<endl;
ans++;
return;
}
for(int i=0;i<n;i++)
{
if(!col[i]&&!dg[i+u]&&!udg[n-u+i])
{
m[u][i]='Q';
col[i]=dg[i+u]=udg[n-u+i]=1;
dfs(u+1);
col[i]=dg[i+u]=udg[n-u+i]=0;//回溯恢复现场
m[u][i]='.';
}
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
m[i][j]='.';
dfs(0);
cout<<ans;
return 0;
}m图着色问题
题目描述
给定无向连通图G和m种不同的颜色,用这些颜色给图的各个顶点着一种颜色,若某种方案使得图中每条边的2个顶点的颜色都不相同,则是一个满足的方案,找出所有的方案。
输入
第一行有3个正整数n,k和m,分别表示n个顶点,k条边,m种颜色
接下来k行,每行2个正整数,表示一条边的两个顶点
输出
所有不同的着色方案数
样例输入
5 8 4
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5样例输出
48提示
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int mp[N][N];
int color[N]={0};
int n,k,m,ans=0;
void dfs(int d)
{
if(d==n+1)
{
ans++;
return;
}
for(int i=1;i<=m;i++)
{
int flag=1;
for(int j=1;j<=n;j++)
{
if(mp[d][j]&&color[j]==i)
{
flag=0;
break;
}
}
if(flag)
{
color[d]=i;
dfs(d+1);
color[d]=0;
}
}
}
int main()
{
cin>>n>>k>>m;
for(int i=0;i<k;i++)
{
int t1,t2;
cin>>t1>>t2;
mp[t1][t2]=1;
mp[t2][t1]=1;
}
dfs(1);
cout<<ans<<endl;
return 0;
}
部分和
题目描述
给定n个整数,判断是否可以从中选择若干数字,使得他们的和恰好为k。
输入
多组测试用例。
对于每组测试用例,第一行一个正整数n,第二行n个整数,第三行一个整数k。
1≤N≤20,输入整数及k均小于1e8。
输出
若可以使得和为k,输出”Yes”,否则”No”。
样例输入
4
1 2 4 7
13样例输出
Yes#include<bits/stdc++.h>
using namespace std;
int s[25];
int n,m;
bool check(int l,int a)
{
if(a==m) return true;
if(l==n) return false;
if(check(l+1,a+s[l]))
return true;
if(check(l+1,a)) return true;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>s[i];
}
cin>>m;
if(check(0,0))
cout<<"YES";
else
cout<<"NO";
return 0;
}本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
